A thought bouncing around in the back of my head related to machine learning algorithm selection is skill vs complexity.
Typically we want the most simplest skillful model, i.e. Occam’s Razor.
A way of thinking about this is to assign a complexity score to a suite of algorithms and then evaluate each in turn.
From this table of data, we can imagine a frontier (or Pareto front) of skill vs complexity.
Come to think of it, I probably got the idea from this AutoGluon slide:
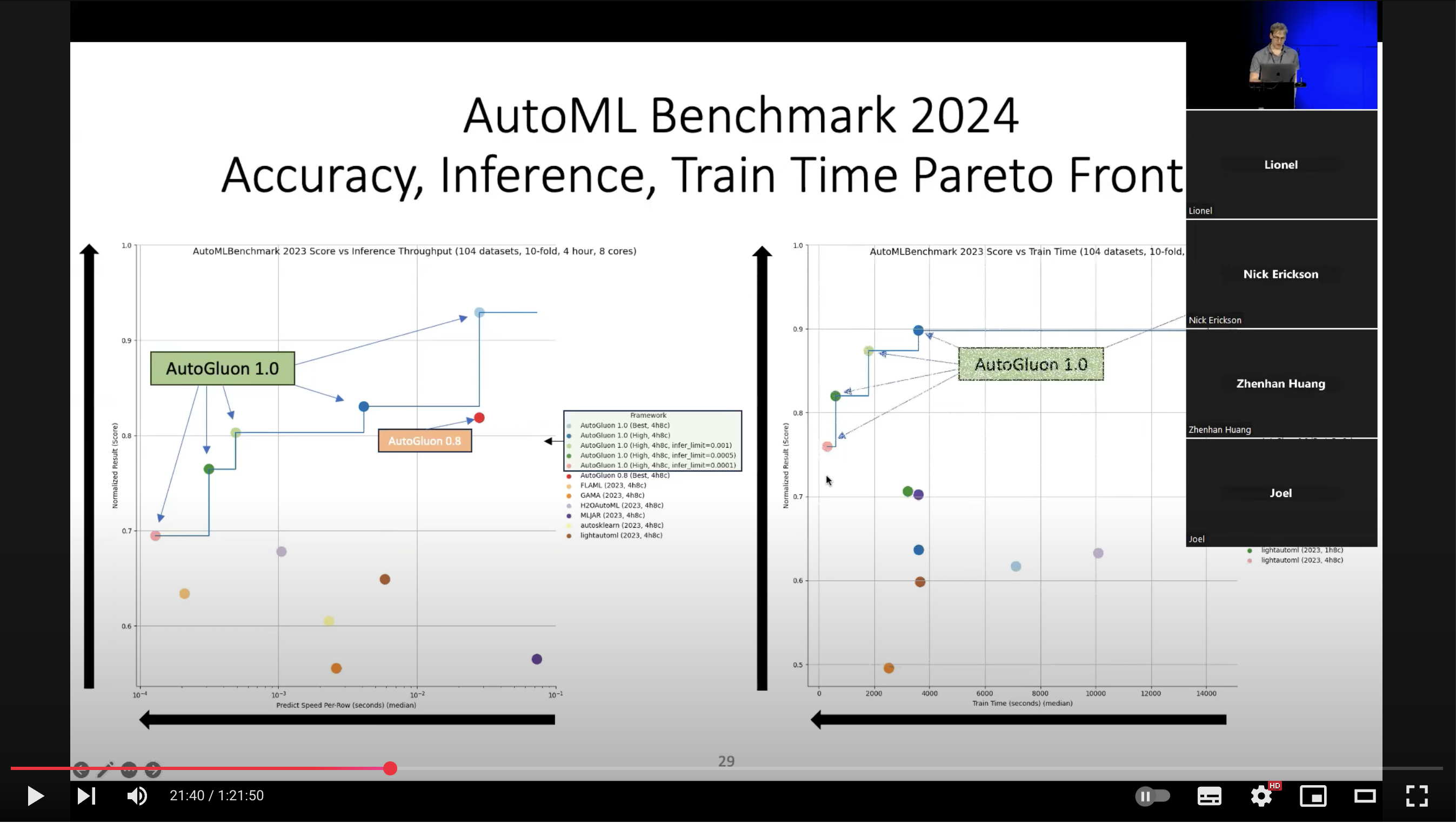
From:
Nevertheless, I often tell ML beginners to test a suite of algorithms with default hyperparameters to quickly find the performance frontier.
This got me thinking, we can estimate the complexity for sklearn algorithms in a standard way, evaluate each algorithm on a problem, then plot the results to give an idea of the frontier of algorithm skill vs complexity?
Some ideas on complexity:
- Time complexity: how long the model takes to eval or train.
- Space complexity: how much memory the fit model requires.
- Model complexity: number of parameters, AIC, BIC, MDL, etc.
I talked with Claude about this and we came up with a somewhat generic class to estimate the complexity of a given sklearn model.
I think it was overkill and I don’t put stock in the results at all.
We then plotted various normalized complexity scores vs performance on a synthetic dataset.
Here are some early results on a classification task showing Accuracy vs BIC:
...
Results:
KNN Performance: 0.950, Complexity: 0.369
SVM Performance: 0.945, Complexity: 0.168
Neural Network Performance: 0.925, Complexity: 0.142
Gaussian Process Performance: 0.925, Complexity: 0.590
Random Forest Performance: 0.920, Complexity: 0.275
Gradient Boosting Performance: 0.880, Complexity: 0.266
Decision Tree Performance: 0.825, Complexity: 0.134
AdaBoost Performance: 0.825, Complexity: 1.122
Logistic Regression Performance: 0.800, Complexity: 0.697
Naive Bayes Performance: 0.795, Complexity: 0.727
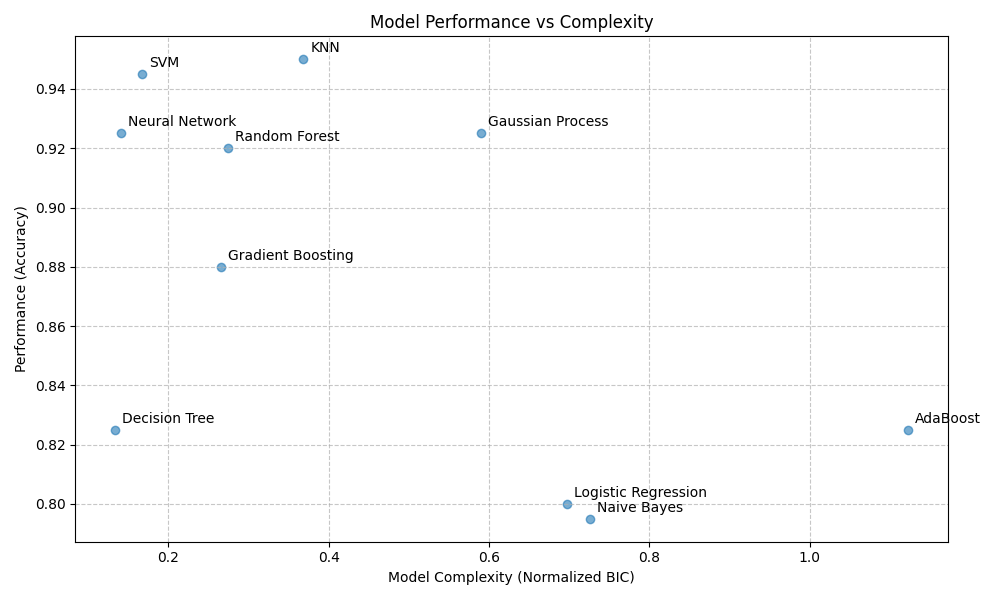
Although I question how we are calculating complexity, there might be merit in the general approach.
The results are directionally reasonable (e.g. we’re aiming for the top left of the plot).
I can imagine this being helpful if we simplify complexity to purely space and/or time.